 |
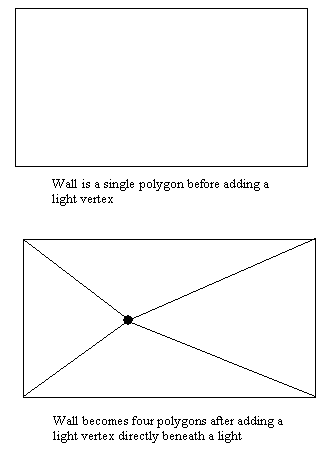
| Figure 1: Adding an extra vertex directly beneath a light. |
It was during my senior year in college that I discovered computer games. Not Wizardry, or Choplifter, or Ultima, because none of those existed yet—the game that hooked me was the original Star Trek game, in which you navigated from one 8x8 quadrant to another in search of starbases, occasionally firing phasers or photon torpedoes. This was less exciting than it sounds; after each move, the current quadrant had to be reprinted from scratch, along with the current stats—and the output device was a 10 cps printball console. A typical game took over an hour, during which nothing particularly stimulating ever happened (Klingons appeared periodically, but they politely waited for your next move before attacking, and your photon torpedoes never missed, so the outcome was never in doubt), but none of that mattered; nothing could detract from the sheer thrill of being in a computer-simulated universe.
Then the college got a PDP-11 with four CRT terminals, and suddenly Star Trek could redraw in a second instead of a minute. Better yet, I found the source code for the Star Trek program in the recesses of the new system, the first time I'd ever seen any real-world code other than my own, and excitedly dove into it. One evening, as I was looking through the code, a really cute girl at the next terminal asked me for help getting a program to run. After I had helped her, eager to get to know her better, I said, "Want to see something? This is the actual source for the Star Trek game!" and proceeded to page through the code, describing each subroutine. We got to talking, and eventually I worked up the nerve to ask her out. She said sure, and we ended up having a good time, although things soon fell apart because of her two or three other boyfriends (I never did get an exact count). The interesting thing, though, was her response when I finally got around to asking her out. She said, "It's about time!" When I asked what she meant, she said, "I've been trying to get you to ask me out all evening—but it took you forever! You didn't actually think I was interested in that Star Trek program, did you?"
Actually, yes, I had thought that, because I was interested in it. One thing I learned from that experience, and have had reinforced countless times since, is that we—you, me, anyone who programs because they love it, who would do it for free if necessary—are a breed apart. We're different, and luckily so; while everyone else is worrying about downsizing, we're in one of the hottest industries in the world. And, so far as I can see, the biggest reason we're in such a good situation isn't intelligence, or hard work, or education, although those help; it's that we actually like this stuff.
It's important to keep it that way. I've seen far too many people start to treat programming like a job, forgetting the joy of doing it, and burn out. So keep an eye on how you feel about the programming you're doing, and if it's getting stale, it's time to learn something new; there's plenty of interesting programming of all sorts to be done. Follow your interests—and don't forget to have fun!
As I've mentioned in previous columns, I've spent the last year and a half working with John Carmack on Quake's 3-D graphics engine. John faced several fundamental design issues while architecting Quake. I've written in past columns about some of those issues, including eliminating non-visible polygons quickly via a precalculated potentially visible set (PVS), and improving performance by inserting potentially visible polygons into a global edge list and scanning out only the nearest polygon at each pixel.
For the rest of this column, I'm going to talk about another, equally crucial design issue: how we developed our lighting approach for the part of the Quake engine that draws the world itself, the static walls and floors and ceilings. Monsters and players are drawn using completely different rendering code, with speed the overriding factor. A primary goal for the world, on the other hand, was to be as precise as possible, getting everything right so that polygons, textures, and sophisticated lighting would be pegged in place, with no visible shifting or distortion under all viewing conditions, for maximum player immersion—all with good performance, of course. As I'll discuss, the twin goals of performance and rock-solid, complex lighting proved to be difficult to achieve with traditional lighting approaches; ultimately, a dramatically different approach was required.
The traditional way to do realistic lighting in polygon pipelines is Gouraud shading (also known as smooth shading). Gouraud shading involves generating a lighting value at each polygon vertex by applying all relevant world lighting, linearly interpolating between lighting values down the edges of the polygon, and then linearly interpolating between the edges of polygon across each span. If texture mapping is desired (all polygons are texture mapped in Quake), then at each pixel in each span, the pixel's corresponding texture map location (texel) is determined, and the interpolated lighting is applied to the texel to generate a final, lit pixel. Texels are generally taken from a 32x32 or 64x64 texture that's tiled repeatedly across the polygon, for several reasons: Performance (a 64x64 texture sits nicely in the 486 or Pentium cache), database size, and less artwork.
The interpolated lighting can consist of either a color intensity value or three separate red, green, and blue values. RGB lighting produces more sophisticated results, such as colored lights, but is slower and best suited to RGB modes. Games like Quake that are targeted at palettized 256-color modes generally use intensity lighting; each pixel is lit by looking up the pixel color in a table, using the texel color and the lighting intensity as the look-up indices.
Gouraud shading allows for decent lighting effects with a relatively small amount of calculation and a compact data set that's a simple extension of the basic polygon model. However, there are several important drawbacks to Gouraud shading, as well.
The quality of Gouraud shading depends heavily on the average size of the polygons being drawn. Linear interpolation is used, so highlights can only occur at vertices, and color gradients are monotonic across the face of each polygon. This can make for bland lighting effects if polygons are large, and makes it difficult to do spotlights and other detailed or dramatic lighting effects. After John brought the initial, primitive Quake engine up using Gouraud shading for lighting, the first thing he tried to improve lighting quality was adding a single vertex and creating new polygons wherever a spotlight was directly overhead a polygon, with the new vertex added directly underneath the light, as shown in Figure 1. This produced fairly attractive highlights, but simultaneously made evident several problems.
 |
| Figure 1: Adding an extra vertex directly beneath a light. |
A primary problem with Gouraud shading is that it requires the vertices used for world geometry to serve as lighting sample points as well, even though there isn't necessarily a close relationship between lighting and geometry. This artificial coupling often forces the subdivision of a single polygon into several polygons purely for lighting reasons, as with the spotlights mentioned above; these extra polygons increase the world database size, and the extra transformations and projections that they induce can harm performance considerably.
Similar problems occur with overlapping lights, and with shadows, where additional polygons are required in order to approximate lighting detail well. In particular, good shadow edges need small polygons, because otherwise the gradient between light and dark gets spread across too wide an area. Worse still, the rate of lighting change across a shadow edge can vary considerably as a function of the geometry the edge crosses; wider polygons stretch and diffuse the transition between light and shadow. A related problem is that lighting discontinuities can be very visible at t-junctions (although ultimately we had to add edges to eliminate t-junctions anyway, because otherwise dropouts can occur along polygon edges). These problems can be eased by adding extra edges, but that increases the rasterization load.
Another problem is that Gouraud shading isn't perspective correct. With Gouraud shading, lighting varies linearly across the face of a polygon, in equal increments per pixel—but unless the polygon is parallel to the screen, the same sort of perspective correction is needed to step lighting across the polygon properly as is required for texture mapping. Lack of perspective correction is not as visibly wrong for lighting as it is for texture mapping, because smooth lighting gradients can tolerate considerably more warping than can the detailed bitmapped images used in texture mapping, but it nonetheless shows up in several ways.
First, the extent of the mismatch between Gouraud shading and perspective lighting varies with the angle and orientation of the polygon being lit. As a polygon turns to become more on-edge, for example, the lighting warps more and therefore shifts relative to the perspective-texture mapped texels it's shading, an effect I'll call viewing variance. Lighting can similarly shift as a result of clipping, for example if one or more polygon edges are completely clipped; I'll refer to this as clipping variance.
These are fairly subtle effects; more pronounced is the rotational variance that occurs when Gouraud shading any polygon with more than three vertices. Consistent lighting for a polygon is fully defined by three lighting values; taking four or more vertices and interpolating between them, as Gouraud shading does, is basically a hack, and does not reflect any consistent underlying model. If you view a Gouraud-shaded quad head-on, then rotate it like a pinwheel, the lighting will shift as the quad turns, as shown in Figure 2. The extent of the lighting shift can be quite drastic, depending on how different the colors at the vertices are.
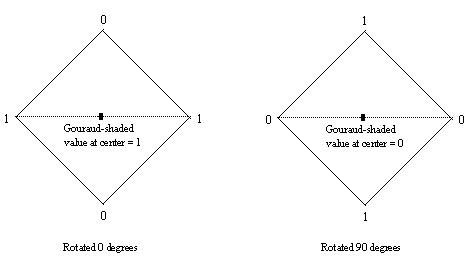 |
| Figure 2: Gouraud shading varies with polygon screen orientation. |
It was rotational variance that finally brought the lighting issue to a head for Quake. We'd look at the floors, which were Gouraud-shaded quads; then we'd pivot, and the lighting would shimmy and shift, especially where there were spotlights and shadows. Given the goal of rendering the world as accurately and convincingly as possible, this was unacceptable.
The obvious solution to rotational variance is to use only triangles, but that brings with it a new set of problems. It takes twice as many triangles as quads to describe the same scene, increasing the size of the world database and requiring extra rasterization, at a performance cost. Triangles still don't provide perspective lighting; their lighting is rotationally invariant, but it's still wrong—just more consistently wrong. Gouraud-shaded triangles still result in odd lighting patterns, and require lots of triangles to support shadowing and other lighting detail. Finally, triangles don't solve clipping or viewing variance.
Yet another problem is that while it may work well to add extra geometry so that spotlights and shadows show up well, that's feasible only for static lighting. Dynamic lighting—light cast by sources that move—has to work with whatever geometry the world has to offer, because its needs are constantly changing.
These issues led us to conclude that if we were going to use Gouraud shading, we would have to build Quake levels from many small triangles, with sufficiently finely-detailed geometry so that complex lighting could be supported and the inaccuracies of Gouraud shading wouldn't be too noticeable. Unfortunately, that line of thinking brought us back to the problem of a much larger world database and a much heavier rasterization load (all the worse because Gouraud shading requires an additional interpolant, slowing the inner rasterization loop), so that not only would the world still be less than totally solid, because of the limitations of Gouraud shading, but the engine would also be too slow to support the complex worlds we had hoped for in Quake.
None of which is to say that Gouraud shading isn't useful in general. Descent uses it to excellent effect, and in fact Quake uses Gouraud shading for moving entities, because these consist of small triangles and are always in motion, which helps hide the relatively small lighting errors. However, Gouraud shading didn't seem capable of meeting our design goals for rendering quality and speed for drawing the world as a whole, so it was time to look for alternatives.
There are many alternative lighting approaches, most of them higher-quality than Gouraud, starting with Phong shading, in which the surface normal is interpolated across the polygon's surface, and going all the way up to ray-tracing lighting techniques in which full illumination calculations are performed for all direct and reflected paths from each light sources for each pixel. What all these approaches have in common is that they're slower than Gouraud shading, too slow for our purposes in Quake. For weeks, we kicked around and rejected various possibilities and continued working with Gouraud shading for lack of a better alternative—until the day John came into work and said, "You know, I have an idea..."
John's idea came to him while was looking at a wall that had been carved into several pieces because of a spotlight, with an ugly lighting glitch due to a t-junction. He thought to himself that if only there were some way to treat it as one surface, it would look better and draw faster—and then he realized that there was a way to do that.
The insight was to split lighting and rasterization into two separate steps. In a normal Gouraud-based rasterizer, there's first an off-line preprocessing step when the world database is built, during which polygons are added to support additional lighting detail as needed, and lighting values are calculated at the vertices of all polygons. At runtime, the lighting values are modified if dynamic lighting is required, and then the polygons are drawn with Gouraud shading.
Quake's approach, which I'll call surface-based lighting, preprocesses differently, and adds an extra rendering step. During off-line preprocessing, a grid, called a light map, is calculated for each polygon in the world, with a lighting value every 16 texels horizontally and vertically. This lighting is done by casting light from all the nearby lights in the world to each of the grid points on the polygon, and summing the results for each grid point. The Quake preprocessor filters the values, so shadow edges don't have a stairstep appearance (a technique suggested by Billy Zelsnack); additional preprocessing could be done, for example Phong shading to make surfaces appear smoothly curved. Then, at runtime, the polygon's texture is tiled into a buffer, with each texel lit according to the weighted average intensities of the four nearest light map points, as shown in Figure 3. If dynamic lighting is needed, the light map is modified accordingly before the buffer, which I'll call a surface, is built. Then the polygon is drawn with perspective texture mapping, with the surface serving as the input texture, and with no lighting performed during the texture mapping.
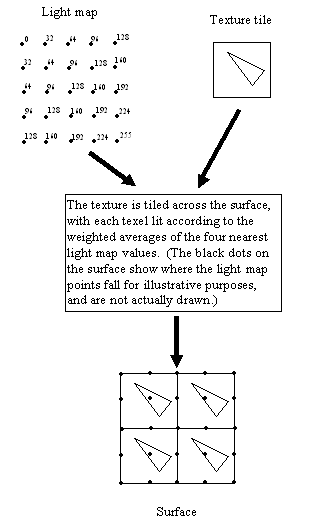 |
| Figure 3: A surface is built by tiling the texture and lighting the texels from the light map. |
So what does surface-based lighting buy us? First and foremost, it provides consistent, perspective-correct lighting, eliminating all rotational, viewing, and clipping variance, because lighting is done in surface space rather than in screen space. By lighting in surface space, we bind the lighting to the texels in an invariant way, and then the lighting gets a free ride through the perspective texture mapper and ends up perfectly matched to the texels. Surface-based lighting also supports good, although not perfect, detail for overlapping lights and shadows. The 16-texel grid has a resolution of two feet in the Quake frame of reference, and this relatively fine resolution, together with the filtering performed when the light map is built, is sufficient to support complex shadows with smoothly fading edges. Additionally, surface-based lighting eliminates lighting glitches at t-junctions, because lighting is unrelated to vertices. In short, surface-based lighting meets all of Quake's visual quality goals, which leaves only one question: How does it perform?
As it turns out, the raw speed of surface-based lighting is pretty good. Although an extra step is required to build the surface, moving lighting and tiling into a separate loop from texture mapping allows each of the two loops to be optimized very effectively, with almost all variables kept in registers. The surface-building inner loop is particular efficient, because it consists of nothing more than interpolating intensity, combining it with a texel and using the result to look up a lit texel color, and storing the results with a dword write every four texels. In assembly language, we've gotten this code down to 2.25 cycles per lit texel in Quake. Similarly, the texture-mapping inner loop, which overlaps an FDIV for floating-point perspective correction with integer pixel drawing in 16-pixel bursts, has been squeezed down to 7.5 cycles per pixel on a Pentium, so the combined inner loop times for building and drawing a surface is roughly in the neighborhood of 10 cycles per pixel. It's certainly possible to write a Gouraud-shaded perspective-correct texture mapper that's somewhat faster than 10 cycles, but 10 cycles/pixel is fast enough to do 40 frames/second at 640x400 on a Pentium/100, so the cycle counts of surface-based lighting are acceptable. It's worth noting that it's possible to write a one-pass texture mapper that does approximately perspective-correct lighting. However, I have yet to hear of or devise such an inner loop that isn't complicated and full of special cases, which makes it hard to optimize; worse, this approach doesn't work well with the procedural and post-processing techniques I'll discuss shortly.
Moreover, surface-based lighting tends to spend more of its time in inner loops, because polygons can have any number of sides and don't need to be split into multiple smaller polygons for lighting purposes; this reduces the amount of transformation and projection that are required, and makes polygon spans longer. So the performance of surface-based lighting stacks up very well indeed—except for caching.
I mentioned earlier that a 64x64 texture tile fits nicely in the processor cache. A typical surface doesn't. Every texel in every surface is unique, so even at 320x200 resolution, something on the rough order of 64,000 texels must be read in order to draw a single scene. (The number actually varies quite a bit, as discussed below, but 64,000 is in the ballpark.) This means that on a Pentium, we're guaranteed to miss the cache once every 32 texels, and the number can be considerably worse than that if the texture access patterns are such that we don't use every texel in a given cache line before that data gets thrown out of the cache. Then, too, when a surface is built, the surface buffer won't be in the cache, so the writes will be uncached writes that have to go to main memory, then get read back from main memory at texture mapping time, potentially slowing things further still. All this together makes the combination of surface building and unlit texture mapping a potential performance problem, but that never posed a problem during the development of Quake, thanks to surface caching.
When he thought of surface-based lighting, John immediately realized that surface building would be relatively expensive. (In fact, he assumed it would be considerably more expensive than it actually turned out to be with full assembly-language optimization.) Consequently, his design included the concept of caching surfaces, so that if the same surface was visible in the next frame, it could be reused without having to be rebuilt.
With surface rebuilding needed only rarely, thanks to surface caching, Quake's rasterization speed is generally the speed of the unlit, perspective-correct texture-mapping inner loop, which suffers from more cache misses than Gouraud-shaded, tiled texture mapping, but doesn't have the overhead of Gouraud shading, and allows the use of larger polygons. In the worst case, where everything in a frame is a new surface, the speed of the surface-caching approach is somewhat slower than Gouraud shading, but generally surface caching provides equal or better performance, so once surface caching was implemented in Quake, performance was no longer a problem—but size became a concern.
The amount of memory required for surface caching looked forbidding at first. Surfaces are large relative to texture tiles, because every texel of every surface is unique. Also, a surface can contain many texels relative to the number of pixels actually drawn on the screen, because due to perspective foreshortening, distant polygons have only a few pixels relative to the surface size in texels. Surfaces associated with partly hidden polygons must be fully built, even though only part of the polygon is visible, and if polygons are drawn back to front with overdraw, some polygons won't even be visible, but will still require surface building and caching. What all this meant was that the surface cache initially looked to be very large, on the order of several megabytes, even at 320x200—too much for a game intended to run on an 8 Mb machine.
Two factors combined to solve this problem. First, polygons are drawn through an edge list with no overdraw, as discussed a few columns back, so no surface is ever built unless at least part of it is visible. Second, surfaces are built at four mipmap levels, depending on distance, with each mipmap level having one-quarter as many texels as the preceding level, as shown in Figure 4. The mipmap level for a given surface is selected to result in a texel:pixel ratio approximately between 1:1 and 1:2, so texels map roughly to pixels, and more distant surfaces are correspondingly smaller. As a result, the number of surface texels required to draw a scene at 320x200 is on the rough order of 64,000; the number is actually somewhat higher, because of portions of surfaces that are obscured and viewspace-tilted polygons, which have high texel-to-pixel ratios along one axis, but not a whole lot higher. Thanks to mipmapping and the edge list, 600K has proven to be plenty for the surface cache at 320x200, even in the most complex scenes, and at 640x480, a little more than 1 Mb suffices.
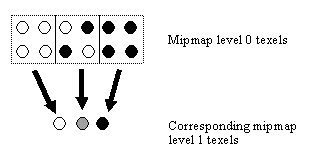 |
| Figure 4: Each texel at a given mipmap level corresponds to four texels at the preceding mipmap level. |
All mipmapped texture tiles are generated as a preprocessing step, and loaded from disk at runtime. One interesting point is that a key to making mipmapping look good turned out to be box-filtering down from one level to the next by averaging four adjacent pixels, then using error diffusion dithering to generate the mipmapped texels.
Also, mipmapping is done on a per-surface basis; the mipmap level for a whole surface is selected based on the distance from the viewer of the nearest vertex. This led us to limit surface size to a maximum of 256x256. Otherwise, surfaces such as floors would extend for thousands of texels, all at the mipmap level of the nearest vertex, and would require huge amounts of surface cache space while displaying a great deal of aliasing in distant regions due to a high texel:pixel ratio.
One final issue with surface caching involves 3-D hardware accelerators. Surfaces are effectively large textures (and larger at the mipmap levels typically used at the high resolutions of accelerators than they are at 320x200), and texture memory tends to be a limited resource on accelerators. Worse, accelerators are built for 16- or 32-bpp graphics, and surfaces are twice as large at 16-bpp as they are at 8-bpp, and correspondingly slower to build. Although the edge list can still be used to cull invisible polygons, it's nonetheless true that a surface cache around 2 Mb is best on a hardware accelerator.
The first generation of accelerators was originally designed for 2 Mb of RAM, which would have been a squeeze, but plummeting memory prices seem to have solved the problem; 4 Mb is fast becoming the standard. And given sufficient memory, surface caching runs at about the same speed on accelerators as Gouraud shading (slower because of building and downloading surfaces, but faster because of fewer, larger polygons), and still offers the same advantage as in software: detailed and consistently correct lighting.
Dynamic lighting has a significant impact on the performance of surface caching, because whenever the lighting on a surface changes, the surface has to be rebuilt. In the worst case, where the lighting changes on every visible surface, the surface cache provides no benefit, and rendering runs at the combined speed of surface building and texture mapping. This worst-case slowdown is tolerable but certainly noticeable, so it's best to design games that uses surface caching so only some of the surfaces change lighting at any one time. If necessary, you could alternate surface relighting so that half of the surfaces change on even frames, and half on odd frames, but large-scale, constant relighting is not surface caching's strongest suit.
Finally, Quake barely begins to tap surface caching's potential. All sorts of procedural texturing and post-processing effects are possible. If a wall is shot, a sprite of pockmarks could be attached to the wall's data structure, and the sprite could be drawn into the surface each time the surface is rebuilt. The same could be done for splatters, or graffiti, with translucency easily supported. These effects would then be cached and drawn as part of the surface, so the performance cost would be much less than effects done by on-screen overdraw every frame. Basically, the surface is a handy repository for all sorts of effects, because multiple techniques can be composited, because it caches the results for reuse without rebuilding, and because the texels constructed in a surface are automatically drawn in perspective.